0/1 Bag Problem Dynamic Processing

Example:

MaxNumber = 4, MaxWeight = 8

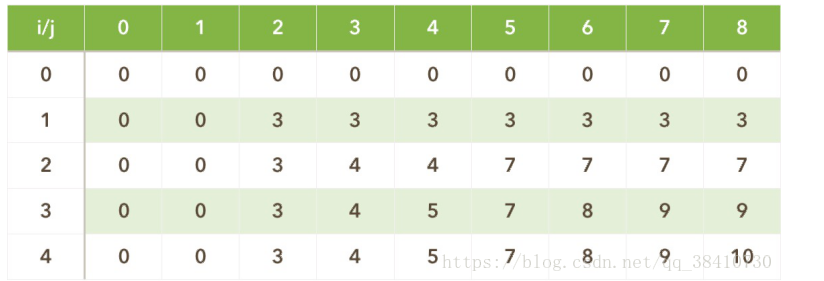
Personal Comprehension:

i 为 只包含前 i 个元素

j 为 包含前 i 个元素中若干个可能得到的重量

V(i, j)的结果是 前 i 个元素在满足小于 j 重量的前提下组合得到的最优质量结果

最重要的是如何获得这样一个最优结果：

1. 逐列进行计算，在同样一个最大承重情况下，要想加入一个元素，首先必须判断其能否放入，其次判断放入一个新元素需要舍弃先前放入的哪些元素

2. 又因为矩阵内先前的结果都是最优解，因此对比之前最优结果中与新元素同样质量的价值，然后判断加入新元素是否为更优解，以此获得最好的部分状态下的结果

3. 同样的逻辑延申到最大重量情况，则得到全局最优结果

#include<iostream>
using namespace std;
#include <algorithm>
 
int w[5] = { 0 , 2 , 3 , 4 , 5 };			//商品的体积2、3、4、5
int v[5] = { 0 , 3 , 4 , 5 , 6 };			//商品的价值3、4、5、6
int bagV = 8;					        //背包大小
int dp[5][9] = { { 0 } };			        //动态规划表
int item[5];					        //最优解情况
 
void findMax() {					//动态规划
	for (int i = 1; i <= 4; i++) {
		for (int j = 1; j <= bagV; j++) {
			if (j < w[i])
				dp[i][j] = dp[i - 1][j];
			else
				dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
		}
	}
}
 
void findWhat(int i, int j) {				//最优解情况
	if (i >= 0) {
		if (dp[i][j] == dp[i - 1][j]) {
			item[i] = 0;
			findWhat(i - 1, j);
		}
		else if (j - w[i] >= 0 && dp[i][j] == dp[i - 1][j - w[i]] + v[i]) {
			item[i] = 1;
			findWhat(i - 1, j - w[i]);
		}
	}
}
 
void print() {
	for (int i = 0; i < 5; i++) {			//动态规划表输出
		for (int j = 0; j < 9; j++) {
			cout << dp[i][j] << ' ';
		}
		cout << endl;
	}
	cout << endl;
 
	for (int i = 0; i < 5; i++)			//最优解输出
		cout << item[i] << ' ';
	cout << endl;
}
 
int main()
{
	findMax();
	findWhat(4, 8);
	print();
 
	return 0;
}

有无进一步压缩矩阵的办法呢？